Sean's Blog

Recently Agostino De Marco posted a video of a Red Bull sponsored aerobatic aircraft flying inverted above a Red Bull Formula 1 car and asked for a guess of the angle of attack (AoA) of the aircraft.

In particular the sign convention for AoA when the aircraft is inverted.

I decided to test out JSBSim to confirm that all the sign conventions worked out in terms of being able to fly the aircraft inverted in trim etc. and to also confirm whether the trim routines could calculate a trim solution for an inverted aircraft.

Although the Red Bull sponsored aerobatic aircraft more than likely has a symmetrical, i.e. uncambered airfoil I decided to make things more interesting in terms of using a cambered airfoil. So I chose the A4 Skyhawk model that is included with JSBSim.

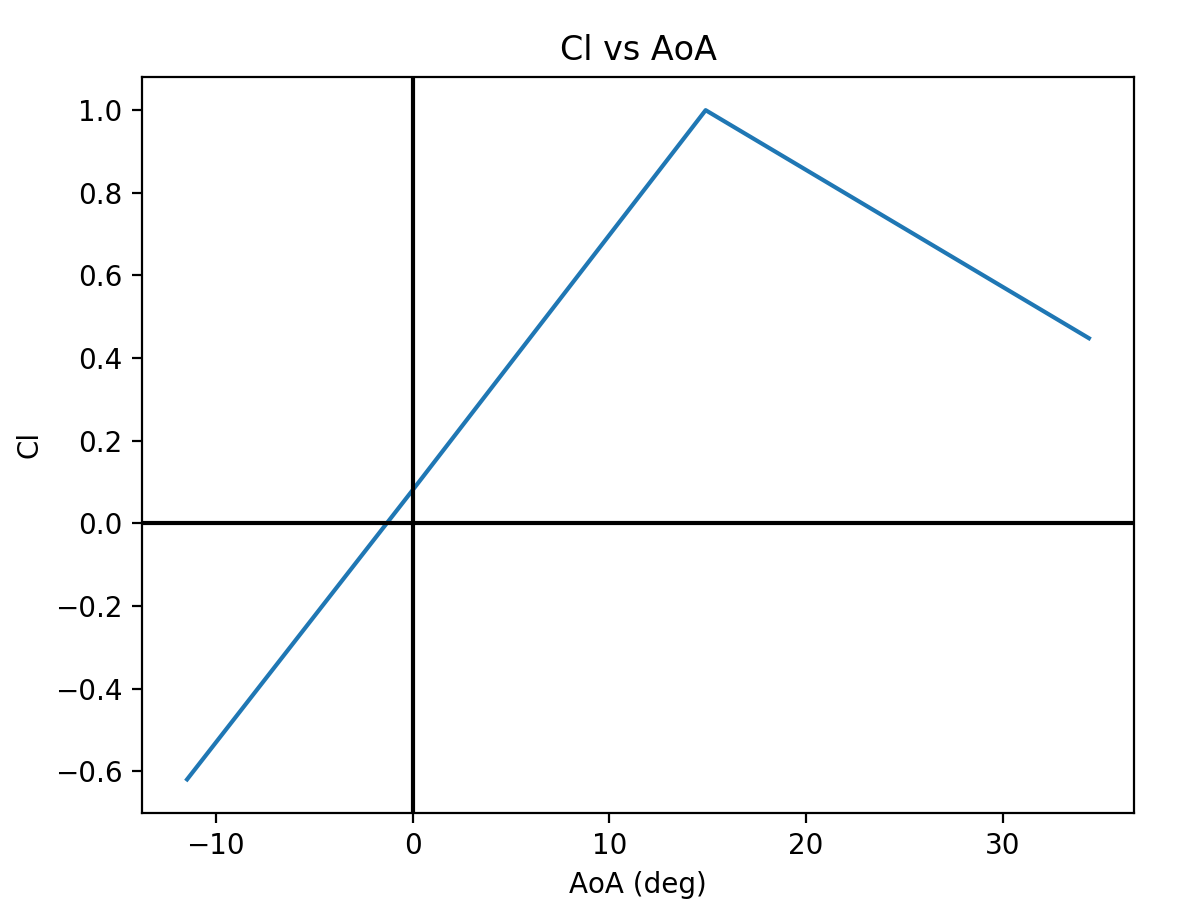
Which has the following Cl vs AoA data.

I then wrote the following Python code to calculate a trim solution for a range airspeeds for both the upright case and the inverted case.

 import jsbsim
 import matplotlib.pyplot as plt
 import math


 fdm = jsbsim.FGFDMExec('..\\') 

 # Load the aircraft 
 fdm.load_model('A4') 

 # Set the engine running
 fdm['propulsion/engine[0]/set-running'] = 1

 # Set alpha range for trim solutions
 fdm['aero/alpha-max-rad'] = math.radians(12)
 fdm['aero/alpha-min-rad'] = math.radians(-12.0)

 results = []

 # Roll angle and label
 configs = [ (0, 'Upright'), (180, 'Inverted') ]

 for config in configs:
    for speed in range(160, 460, 10):
        fdm['ic/h-sl-ft'] = 250
        fdm['ic/vc-kts'] = speed
        fdm['ic/gamma-deg'] = 0
        fdm['ic/phi-deg'] = config[0]

        # Initialize the aircraft with initial conditions
        fdm.run_ic() 

        fdm.run()

        # Trim
        try:
            fdm['simulation/do_simple_trim'] = 1
            results.append((fdm['velocities/vc-kts'], fdm['aero/alpha-deg']))
        except RuntimeError as e:
            # The trim cannot succeed. Just make sure that the raised 
            # exception is due to the trim failure otherwise rethrow.
            if e.args[0] != 'Trim Failed':
                raise

    speed, alpha = zip(*results)
    plt.plot(speed, alpha, label=config[1])

 plt.xlabel('IAS (kt)')
 plt.ylabel('AoA (deg)')
 plt.title('AoA vs IAS')
 plt.legend()

 plt.show()

Sure enough JSBSim didn’t have any issues calculating trim solutions for the inverted case.

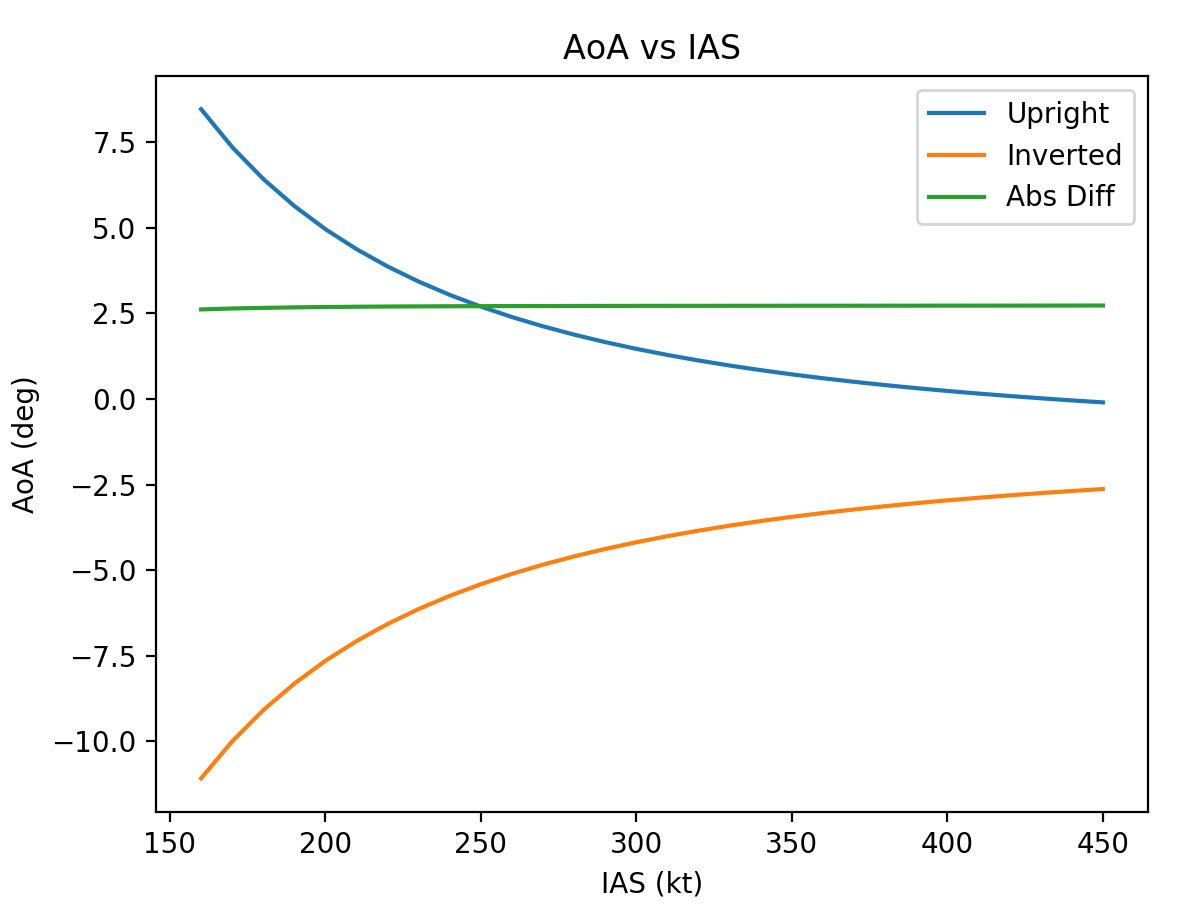
The difference of ~2.7°, i.e. the slightly larger AoA required for the inverted case pretty much matches the negative AoA required to achieve the same absolute Cl achieved at 0° AoA, i.e. where the Cl vs AoA line crosses the y-axis.

This difference will vary depending on the airfoil in terms of the slope of the Cl vs AoA line and where it crosses the y-axis. In the case of a symmetrical, i.e. non-cambered airfoil the Cl vs AoA will pass through the origin so there won’t be a difference in the absolute AoA required for upright versus inverted flight.