Pitch Rate Damping - JSBSim Test

Fri Feb 02, 2018

When an aircraft pitches up or down the tailplane rotates around the cg of the aircraft and this motion causes a change in the tailplane’s angle of attack, which generates a change in lift at the tailplane. This change in lift at the tailplane in conjunction with the tailplane’s arm from the cg generates an opposing, or damping, pitching moment.

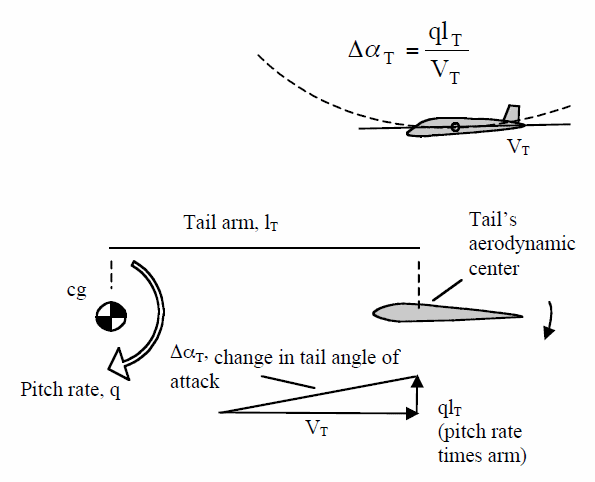
image alt text

The pitch rate damping moment is proportional to the length of the tail arm and the change in lift. The change in lift is proportional to the change in the angle of attack which is proportional to the pitch rate and inversely proportional to the true airspeed.

The moment due to pitch rate is:

$$M_q = \frac{1}{2} \rho V^2 S \bar{c} C_{m_q} \frac{q \bar{c}}{2V} $$

$M_q = \frac{1}{2} \rho V^2 S \bar{c} C_{m_q} \frac{q \bar{c}}{2V}$

$$M_q = C_{m_q} \frac{\rho V S \bar{c}^2}{4} q$$

$M_q = C_{m_q} \frac{\rho V S \bar{c}^2}{4} q$

Unlike some of the other longitudinal moments, like the moment due to alpha which relates to static stability, the pitch rate moment in addition to being proportional to the dynamic pressure is also inversely proportional to the TAS.

As the TAS increases the change in the tailplane’s angle of attack for the same pitch rate is smaller.

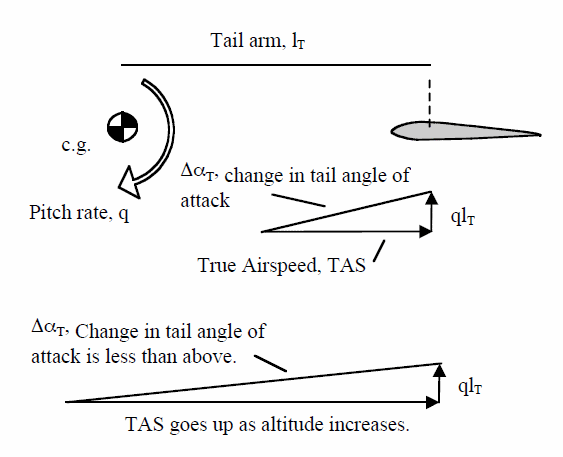
image alt text

This means that flying at the same IAS (same dynamic pressure) at different altitudes results in a different pitch rate damping, i.e. for the same IAS at a higher altitude the pilot will experience less pitch rate damping.

I’m going to test this out in JSBSim with the Boeing 737 model. Here is the relevant snippet from the 737’s aerodynamics section for specifying the aerodynamic moments. In this case $C_{m_q}$ has a value of -27.

<function name="aero/coefficient/Cmq">
    <description>Pitch_moment_due_to_pitch_rate</description>
    <product>
        <property>aero/qbar-psf</property>
        <property>metrics/Sw-sqft</property>
        <property>metrics/cbarw-ft</property>
        <property>aero/ci2vel</property>
        <property>velocities/q-aero-rad_sec</property>
        <value>-27.0</value>
    </product>
</function>

The aircraft is trimmed at an IAS of 250kt at 3,000ft and then an elevator step input is applied. The same test is then performed at 30,000ft.

   Altitude    IAS      TAS      Mq (lb.ft per 1 degree/s pitch rate)
   3,000ft     250kt    261kt    -20,016
   30,000ft    250kt    393kt    -12,369

So the pitch rate damping moment at 30,000ft is approximately 62% of the pitch rate damping motion at 3,000ft.

Now for some graphs comparing the response of the aircraft to the same elevator step input at 3,000ft and at 30,000ft.

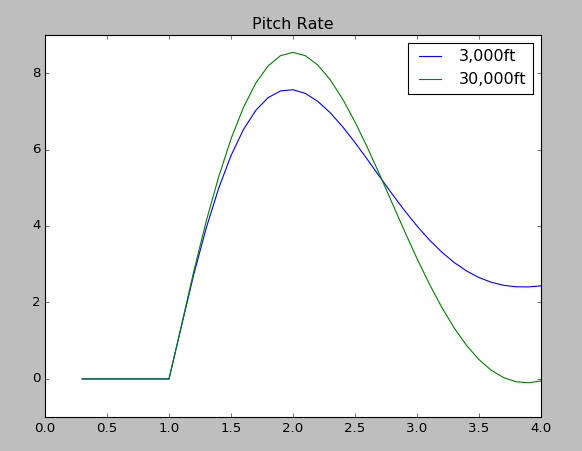
image alt text

With lower pitch rate damping moment the aircraft’s pitch rate increases more rapidly at 30,000ft and achieves a higher maximum pitch rate.

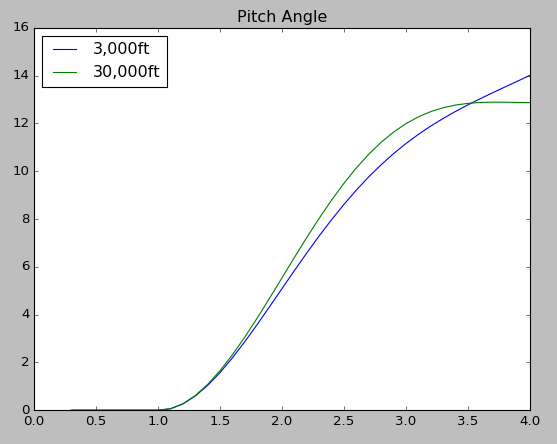
image alt text

The pitch angle also increases more rapidly at 30,000ft.

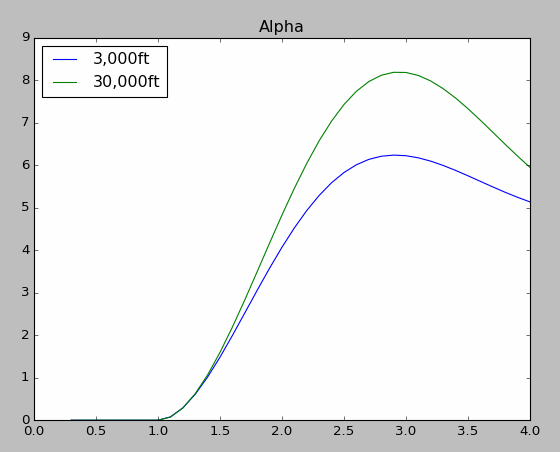
image alt text

The lower pitch rate damping at 30,000ft also means that the angle of attack increases at a faster rate at 30,000ft compared to at 3,000ft.

The higher alpha will result in a greater $C_{m_\alpha}$ restoring moment diminishing the lower pitch rate damping moment to some degree.

$$M_\alpha = \frac{1}{2} \rho V^2 S \bar{c} C_{m_\alpha} \alpha$$

$M_\alpha = \frac{1}{2} \rho V^2 S \bar{c} C_{m_\alpha} \alpha$

An illustration of the various pitching moments for the aircraft at 30,000ft.

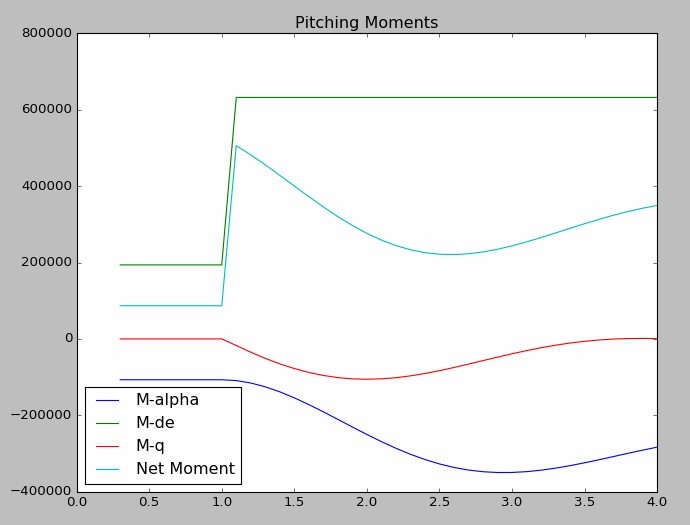
image alt text

The reason the net moment isn’t exactly 0 while the aircraft is in trim up until the elevator step input at time 1.0 is because the aerodynamic reference point (AeroRP) for the aerodynamic forces and moments isn’t coincident with the cg, in addition to other pitching moments from the engines for example.