Sean's Blog

In the mid 1980s while I was in high school my father bought me an Apple II, well actually a clone of an Apple II from Hong Kong. He had been a helicopter pilot in the air force and had then become an airline pilot, hence the Hong Kong connection.

I had always had an interest in aircraft and so one of the first programs I wrote for the Apple II was a very basic aircraft simulator based on formulas in Mechanics of Flight and some basic high school trigonometry.

Recently I came across a talk given by Michael Tiller titled - Modelica: Component-Oriented Modeling of Physical Systems which describes the Modelica language and tools which allow you to describe a physical system by listing the equations involved. As long as the number of variables involved equals the number of equations then Modelica can simulate the model. He also has a free online book describing Modelica - Modelica by Example.

So I downloaded the free open source version of Modelica - OpenModelica to test it out. For an initial basic test I decided to model a simple rocket launch. Three forces are modeled, namely the thrust from the rocket engine which is constant while it has fuel, aerodynamic drag both on the way up and on the way down and the gravitational force on the rocket which varies since the fuel mass decreases as it’s burnt by the engine.

In terms of the aerodynamic drag the assumption is made that as the rocket reaches it’s maximum trajectory it flips over 180 degrees to come down nose first so that the coefficient of drag used is the same for the ascent and the descent. I also assume that the rocket won’t be flying very high so we can assume a constant air density.

Forces acting on the rocket.

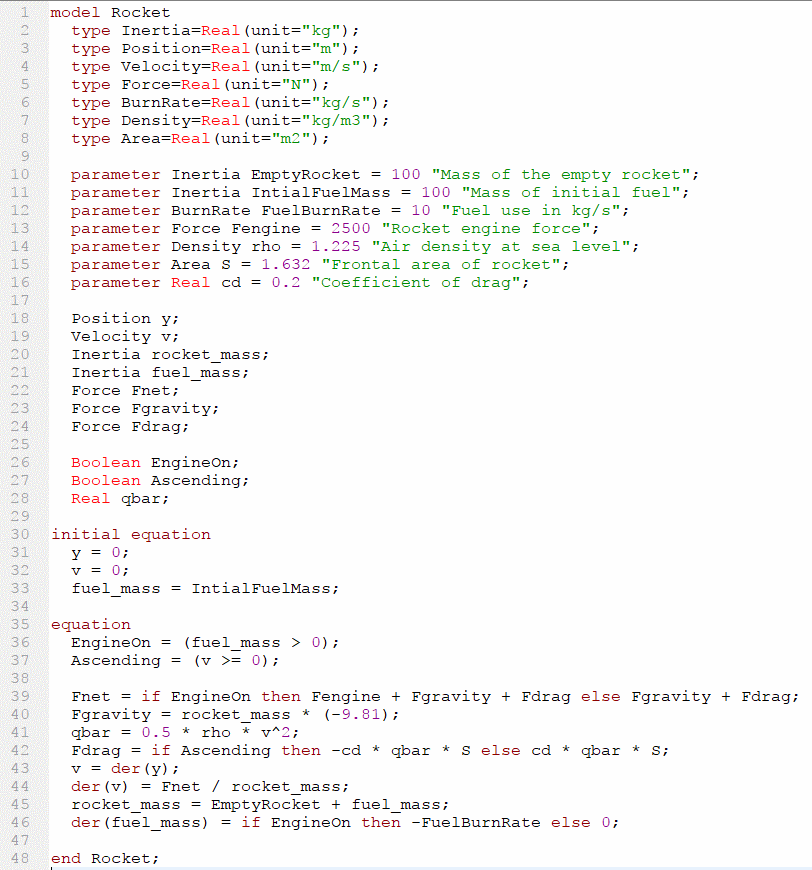
Here is the Modelica code to model the rocket system, the heart of which are the seven equations describing the forces and calculating the rocket’s mass based on the fuel consumption.

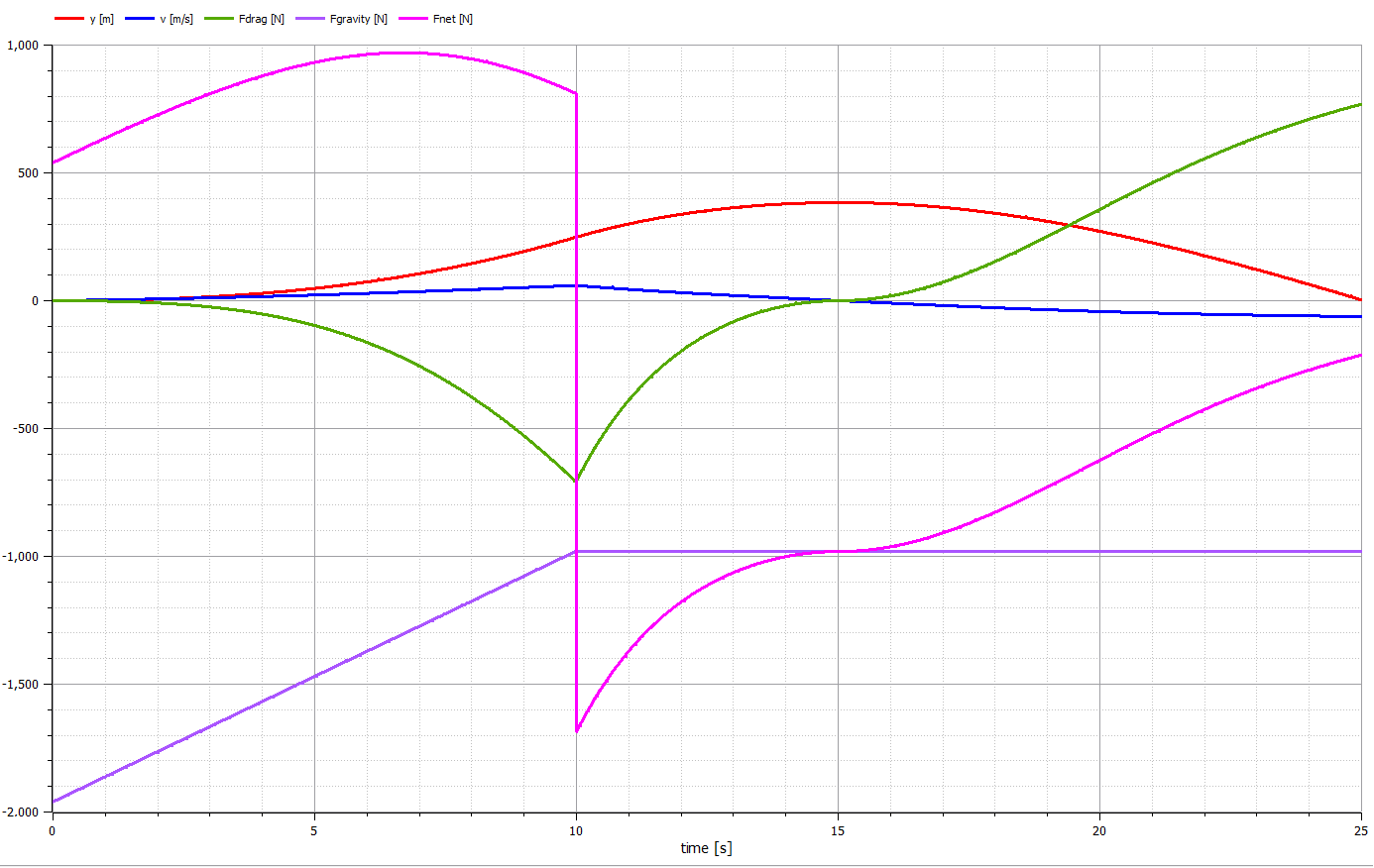
Here is a graph showing most of the variables (forces, velocity and height) over the course of the simulation run. Click on the graph for a full size version.

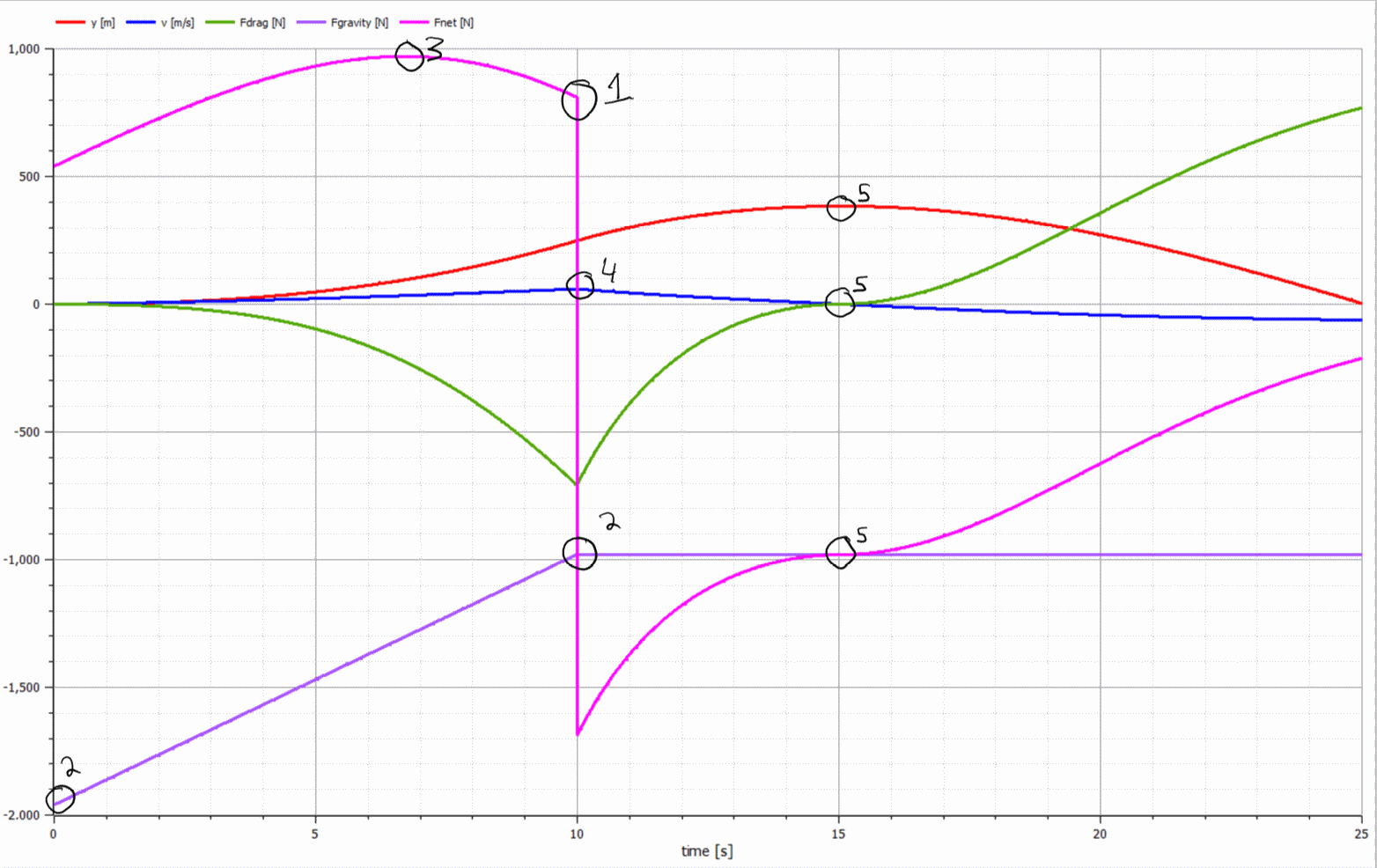
Here is an annotated version of the graph with some sanity checks. Click on the graph for a full size version.

1. Engine cut-off. The model starts with 100kg of fuel and a fuel burn rate of 10kg/s so we expect engine cut-off at exactly 10 seconds. At 10s we see the net force flips from being positive, i.e. the engine force is greater than the gravitational force and drag force to being negative since the engine has cut out. Leaving only drag and gravity acting on the rocket.

2. Gravitational force. Note how the gravitational force decreases from time 0s when the rocket is full of fuel to time 10s when the fuel is all used up.

3. Maximum net force. Is a trade-off between the rocket motor force which is constant and the gravitational force which decreases as fuel is burnt versus the increasing drag force which increases with the square of the velocity. After this point the drag force starts to dominate.

4. Maximum velocity. Reached as the rocket motor shuts off. Also maximum drag force at the same time.

5. Apogee. Reached as the velocity goes to 0, drag also goes to 0 at this instant and the net force is gravity only.

By simply changing some of the parameters of the model, e.g. the fuel burn rate or the initial amount of fuel etc. you can quickly see what effect that has by re-running the simulation.